本文目录导读:
空间直线的方向向量求解方法探究
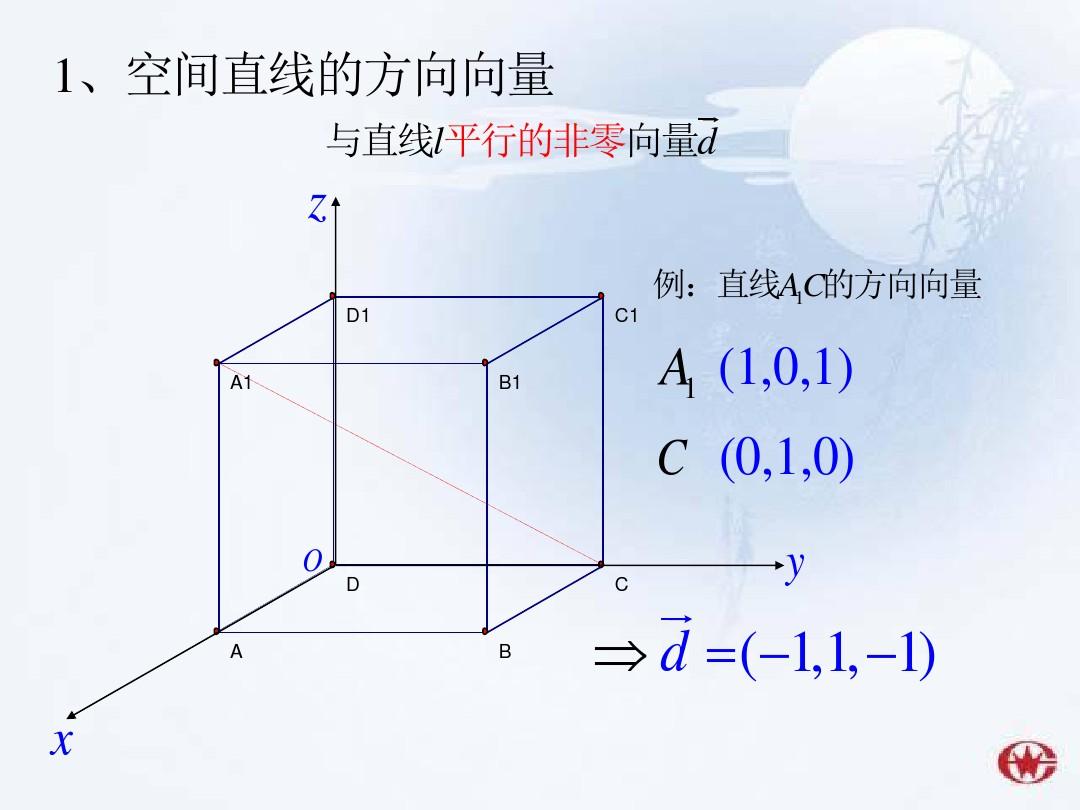
在三维空间中,直线作为一种基本的几何元素,其方向性是其重要的属性之一,为了准确描述直线的方向,我们引入了方向向量的概念,方向向量是一个与直线平行的非零向量,它不仅能够表示直线的方向,还能帮助我们进行各种与直线相关的计算,本文将详细介绍空间直线的方向向量的求解方法,并通过实例进行说明。
空间直线的方向向量定义
在三维空间中,一条直线可以由一个点和一个方向向量唯一确定,假设直线L经过点P(x0, y0, z0),其方向向量为v=(l, m, n),则直线L可以表示为:
L: (x - x0) / l = (y - y0) / m = (z - z0) / n
(l, m, n)是方向向量的三个分量,它们分别表示直线在x、y、z轴上的方向分量,需要注意的是,方向向量只关心直线的方向,而不关心其位置,对于同一条直线,可以有无数个方向向量,但它们都平行于彼此。
空间直线的方向向量求解方法
1、两点法
在三维空间中,通过两点可以确定一条直线,假设直线L上有两个点A(x1, y1, z1)和B(x2, y2, z2),则直线L的方向向量可以通过以下步骤求得:
(1)计算两点之间的差向量AB:
AB = (x2 - x1, y2 - y1, z2 - z1)
(2)将差向量AB单位化,得到方向向量v:
v = AB / |AB|
|AB|是差向量AB的模长,可以通过以下公式计算:
|AB| = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)

方向向量v可以表示为:
v = ((x2 - x1) / |AB|, (y2 - y1) / |AB|, (z2 - z1) / |AB|)
2、参数方程法
如果已知直线的参数方程,也可以直接从中得到方向向量,假设直线的参数方程为:
x = x0 + at
y = y0 + bt
z = z0 + ct
(x0, y0, z0)是直线上的一点,(a, b, c)是参数,t是参数变量,则直线的方向向量v可以表示为:
v = (a, b, c)
这是因为参数方程中的参数系数(a, b, c)实际上表示了直线在x、y、z轴上的方向分量。
3、点向式方程法
如果已知直线的点向式方程,也可以从中得到方向向量,点向式方程的一般形式为:
(x - x0) / l = (y - y0) / m = (z - z0) / n
(x0, y0, z0)是直线上的一点,(l, m, n)是方向向量的三个分量,方向向量v可以直接从点向式方程中读出:
v = (l, m, n)
4、两平面交线法
如果直线是两平面的交线,则直线的方向向量垂直于两平面的法向量,通过计算两法向量的叉积,即可得到直线的方向向量,假设两平面的法向量分别为n1和n2,则直线的方向向量v可以通过以下公式计算:
v = n1 × n2
×表示向量的叉积运算。
实例分析
为了更好地理解空间直线的方向向量的求解方法,我们通过一个实例进行说明,假设直线L经过点A(1, 2, 3)和点B(4, 5, 6),求直线L的方向向量。

根据两点法,我们首先计算两点之间的差向量AB:
AB = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3)
我们计算差向量AB的模长|AB|:
|AB| = √(3^2 + 3^2 + 3^2) = 3√3
我们将差向量AB单位化,得到方向向量v:
v = (3 / (3√3), 3 / (3√3), 3 / (3√3)) = (1 / √3, 1 / √3, 1 / √3)
直线L







发表评论