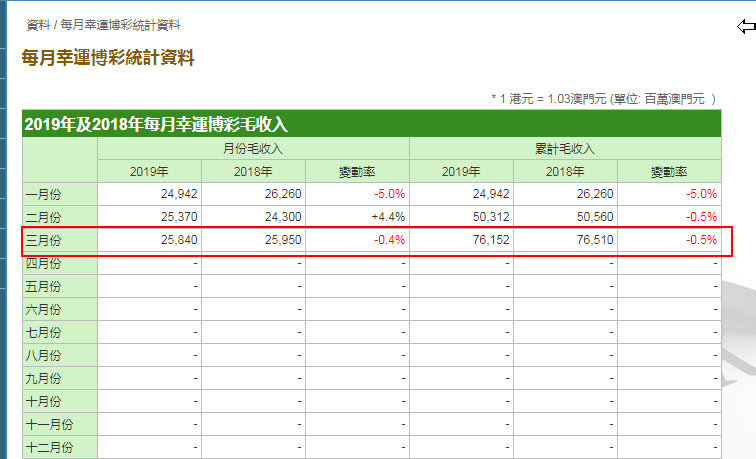
本文目录导读:
深入解析与实例应用
在数学和物理学的许多领域中,斜率(Slope)是一个至关重要的概念,它描述了直线或曲线上某一点的倾斜程度,即该点处函数值随自变量变化的快慢,斜率不仅在数学中有着重要的地位,而且在日常生活和工程实践中也有着广泛的应用,本文将详细解析斜率的计算方法,并通过实例加深理解。
斜率的定义
斜率,通常用字母k表示,是描述直线或曲线上某一点倾斜程度的量,在二维坐标系中,斜率定义为直线与x轴正方向夹角的正切值,即k=tan(α),为直线与x轴的夹角,对于一次函数y=kx+b(k≠0),斜率k就是该函数的系数。
斜率的计算方法
1、两点式斜率公式
两点式斜率公式是最常用的斜率计算方法,对于直线上的任意两点(x1, y1)和(x2, y2),斜率k可以通过以下公式计算:
k = (y2 - y1) / (x2 - x1)
这个公式适用于任何直线,包括水平线和垂直线,当直线与x轴平行时,斜率k=0;当直线与y轴平行时,斜率不存在(因为分母为0)。
2、一次函数斜率
对于一次函数y=kx+b(k≠0),斜率k就是该函数的系数,这个公式直接给出了斜率与函数系数之间的关系,使得我们可以直接通过函数表达式求出斜率。
3、曲线在某点的斜率
对于曲线上的某一点,我们可以利用导数的概念来求斜率,导数描述了函数在某一点处函数值随自变量变化的快慢,即该点的斜率,对于可导函数f(x),在点x0处的斜率k可以通过求导并代入x0得到:
k = f'(x0)
斜率的性质
1、斜率与倾斜角的关系
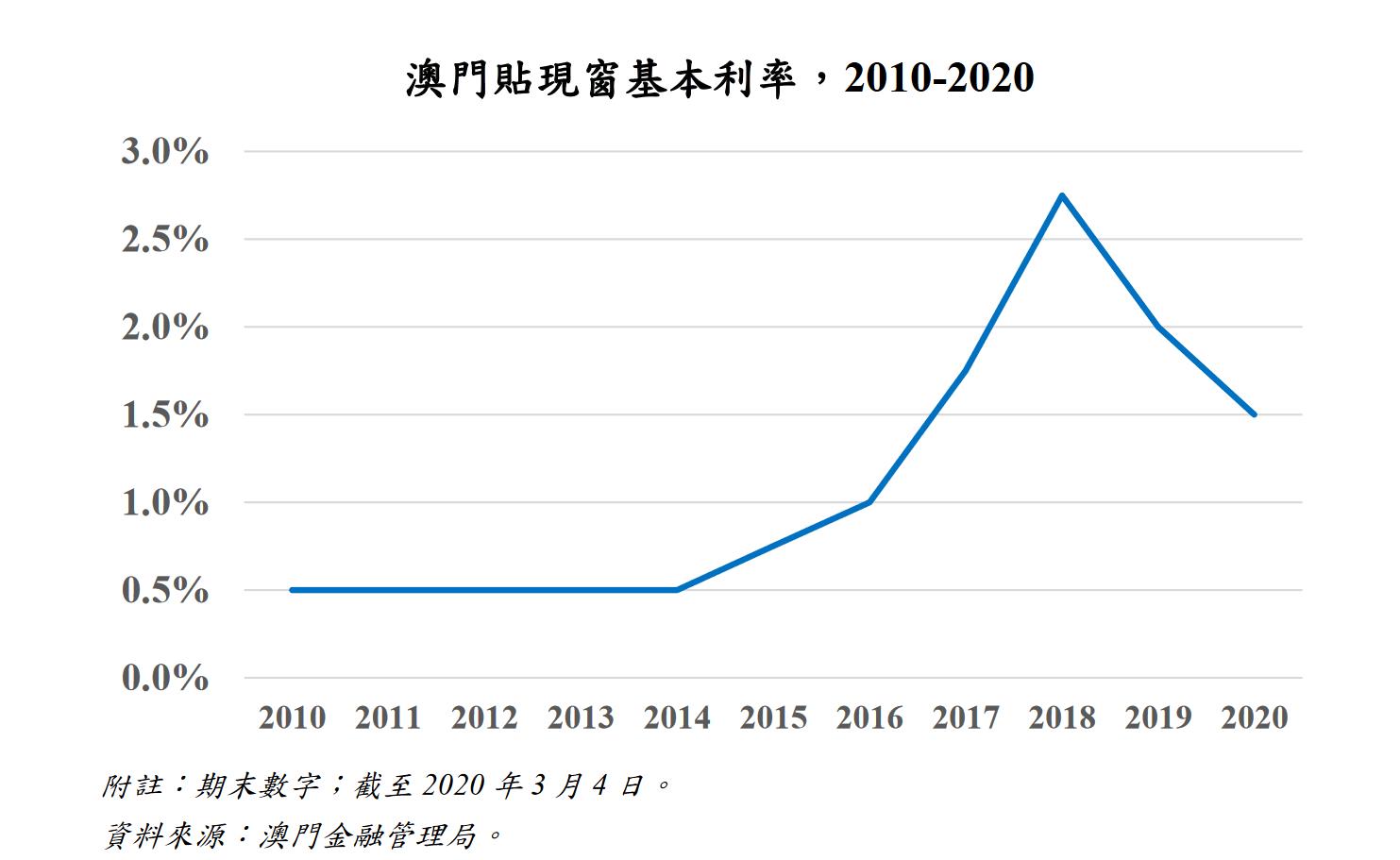
斜率k与直线与x轴的夹角α之间的关系为k=tan(α),当α在0°到90°之间时,k为正数,表示直线向上倾斜;当α在90°到180°之间时,k为负数,表示直线向下倾斜;当α=0°或180°时,k=0,表示直线与x轴平行;当α=90°时,斜率不存在。
2、斜率与平行线和垂直线的关系
两条直线平行当且仅当它们的斜率相等;两条直线垂直当且仅当它们的斜率乘积为-1(或一条直线斜率为0,另一条直线斜率不存在),这些性质在几何学和解析几何中有着广泛的应用。
实例应用
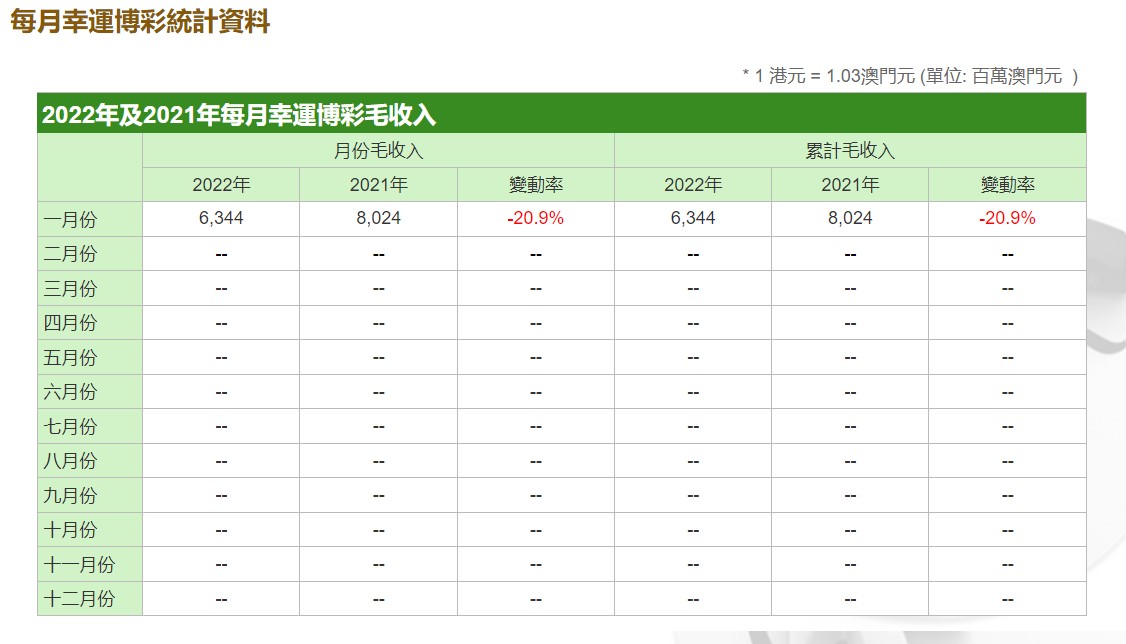
1、经济学中的斜率
在经济学中,斜率常用于描述供需曲线,在需求曲线中,斜率表示价格变动对需求量的影响程度,当需求曲线较陡峭时(斜率较大),价格变动对需求量的影响较小;当需求曲线较平缓时(斜率较小),价格变动对需求量的影响较大,类似地,在供给曲线中,斜率表示价格变动对供给量的影响程度。
2、物理学中的斜率
在物理学中,斜率常用于描述物理量与时间、距离等变量之间的关系,在速度-时间图像中,斜率表示加速度;在位移-时间图像中,斜率表示速度,这些关系在力学、电磁学等领域中有着广泛的应用。
3、图像处理中的斜率
在图像处理中,斜率常用于描述图像边缘的倾斜程度,通过计算图像中相邻像素点之间的斜率变化,可以检测出图像中的边缘信息,这对于图像分割、目标检测等任务具有重要意义。
斜率作为数学和物理学中的一个基本概念,具有广泛的应用价值,通过本文的介绍,我们了解了斜率的定义、计算方法、性质以及在不同领域中的应用,在实际应用中,我们需要根据具体问题选择合适的斜率计算方法,并充分利用斜率的性质进行分析和推理,我们也需要认识到斜率与其他数学概念之间的联系和区别,以便更好地理解和应用斜率这一概念。







发表评论